1、矩形、菱形、正方形的性质1.矩形的性质①具备平行四边形的所有性质;②矩形的四个角都是直角;③矩形的对角线相等;④矩形是轴对称图形,它有两条对称轴;⑤直角三角形斜边上的中线等于斜边的一半。2.菱形的性质①具备平行四边形的所有性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,每条对角线所在的直线都是它的对称轴;⑤菱形的面积=底高=对角线乘积的一半。3.正方形的性质正方形具备平行四边形,矩形,菱形的所有性质①边:四边相等,对边平行;②角:四个角都是直角;③对角线:互相平分;相等;且垂直;每一条对角线平分一组对角,即正方形的对角线与边的夹角为45度;④正方形是轴对称图形,有四条对称轴。例1 矩形ABCD中,DEAC于E,且ADE:EDC=3:2,则BDE的度数为 ( )A.360B.90C.270D.180
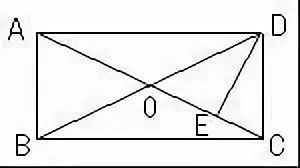
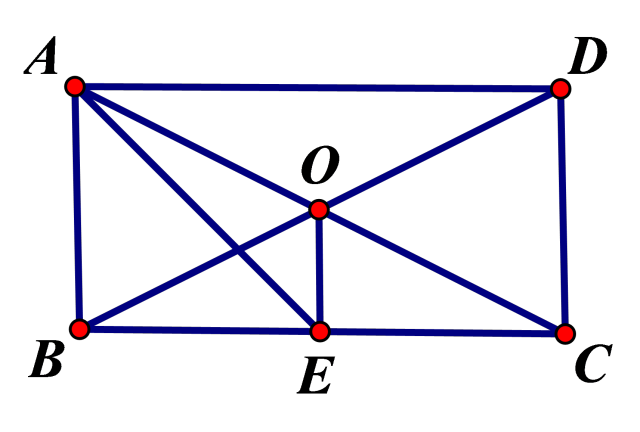
例2 如图,矩形ABCD中,AEBD于点E,对角线AC与BD相交于点O,BE:ED=1:3,AB=6cm,求AC的长。例3 如图, O是矩形ABCD 对角线的交点, AE平分 BAD,AOD=120 ,求AEO 的度数。
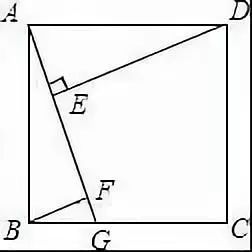
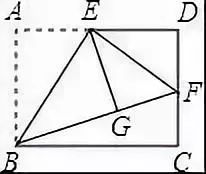
例4 菱形的周长为40cm,两邻角的比为1:2,则较短对角线的长________ 。例5 如图,在正方形ABCD中,G是BC上任意一点,连接AG,DEAG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数目关系,并说明理由.
2、矩形、菱形、正方形的断定1.矩形的断定①有一个内角是直角的平行四边形是矩形;②对角线相等的平行四边形是矩形;③有三个角是直角的四边形是矩形;④还有对角线相等且互相平分的四边形是矩形。2.菱形的断定办法①有一组邻边相等的平行四边形是菱形;②对角线互相垂直的平行四边形是菱形;③四条边都相等四边形是菱形;④对角线垂直平分的四边形是菱形。3.正方形的断定①菱形+矩形的一条特点;②菱形+矩形的一条特点;③平行四边形+一个直角+一组邻边相等。说明一个四边形是正方形的一般思路是:先判断它是矩形,在判断这个矩形也是菱形;或先判断它是菱形,再判断这个菱形也是矩形。例1. 如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,并交于点E,连续EC、AD。
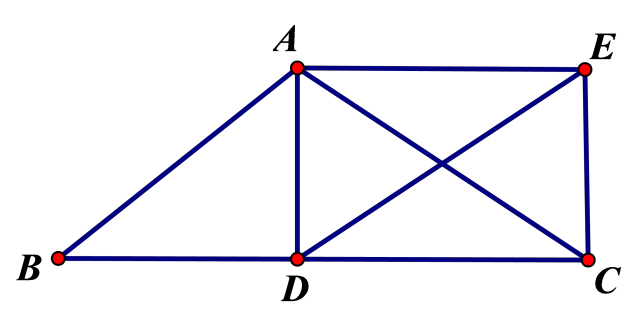
求证:四边形ADCE是矩形。例2.如图,△ABC中,C=90,AD平分BAC,EDBC,DF//AB.求证:AD与EF互相垂直平分。
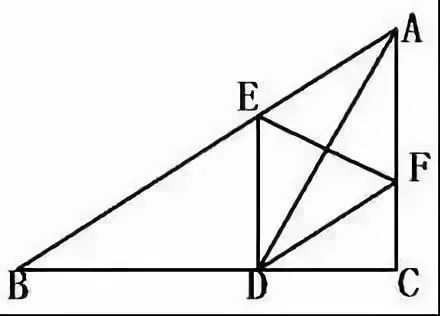
例3.已知如图,在△ABC,ACB=900,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF∥BC。求证:四边形CDEF是菱形。
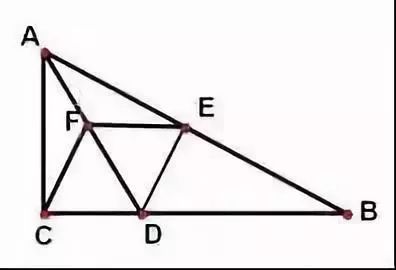
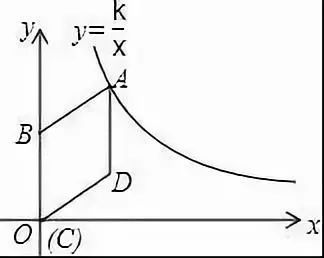
3、矩形、菱形、正方形与函数综合题1.借助矩形、菱形、正方形的常识解决函数问题;2.借助函数常识解决矩形、菱形、正方形的问题;例1.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比率函数y=(k>0,x>0)的图象上,点D的坐标为(4,3).(1)求k的值;(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离。
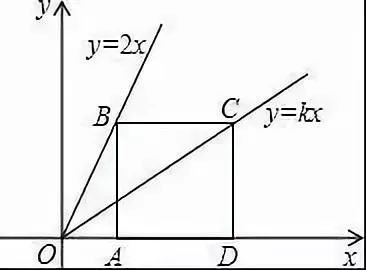
例2.如图,点B、C分别在两条直线y=2x和y=kx上,点A、D是x轴上两点,已知四边形ABCD是正方形,则k值为______.
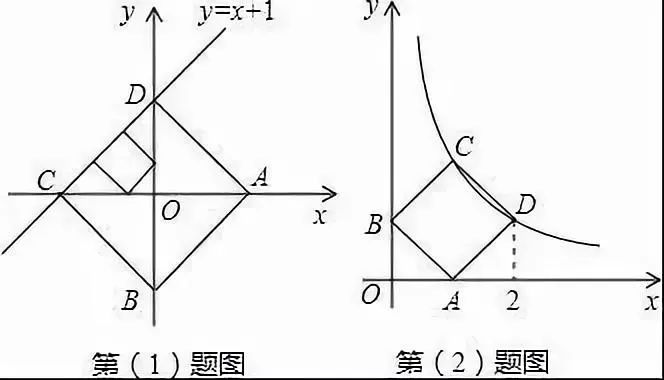
例3 已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.比如:如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;(2)若某函数是反比率函数,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比率函数图象上,求m的值及反比率函数分析式。
4、矩形、正方形的翻折1.从翻折中找出对称轴,借助对称性找相等关系。2.借助相等关系打造方程解决问题。例1 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长是( )A.36 B.26C.25 D.23
例2 如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B落在ADC的角平分线上时,则点B到BC的距离为()A.1或2 B. 2或3C.3或4 D. 4或5
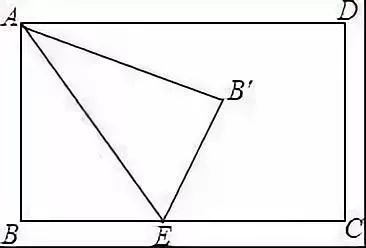
例3 如图,在边长为1的正方形ABCD中,E为AD边上一点,连接BE,将△ABE沿BE对折,A点恰好落在对角线BD上的点F处。延长AF,与CD边交于点G,延长FE,与BA的延长线交于点H,则下列说法:①△BFH为等腰直角三角形;②△ADF≌△FHA; ③DFG=60;④DE=2-2;⑤S△AEF=S△DFG.其中正确的说法有( )A.1个B.2个C.3个 D.4个
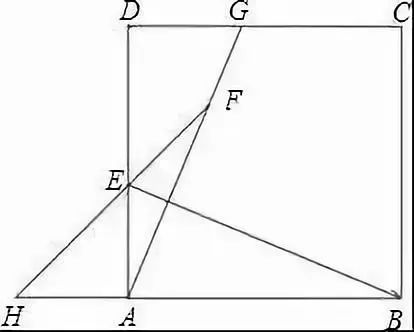
例4 四边形ABCD是正方形,MAN=45,它的两边AM、AN分别交CB、DC与点M、N,连接MN,作AHMN,垂足为点H。(1)如图1,猜想AH与AB有哪些数目关系?并证明。(2)如图2,已知BAC=45,ADBC于点D,且BD=2,CD=3,求AD的长。
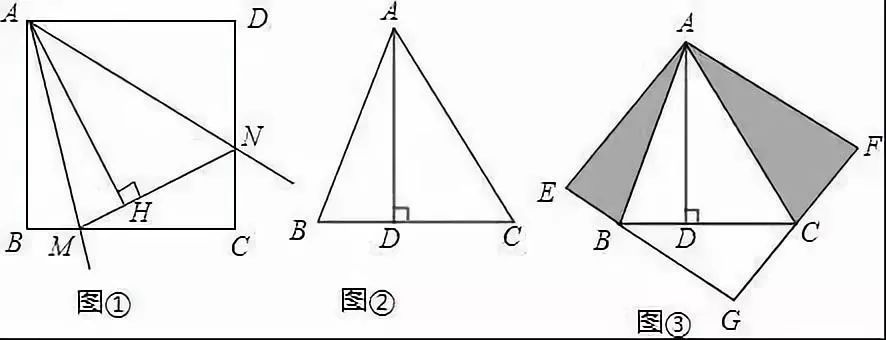
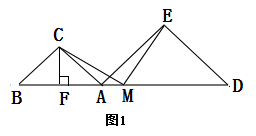
5、综合运用1.计算。借助矩形、菱形、正方形中的等腰三角形和直角三角形进行计算。2.证明。借助矩形、菱形、正方形的性质和断定,结合全等三角形、等腰三角形、等边三角形的常识展开证明。3.探究。借助矩形、菱形、正方形等常识展开探究。例1 在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1地方放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DGBE,请你帮他说明理由.(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由。
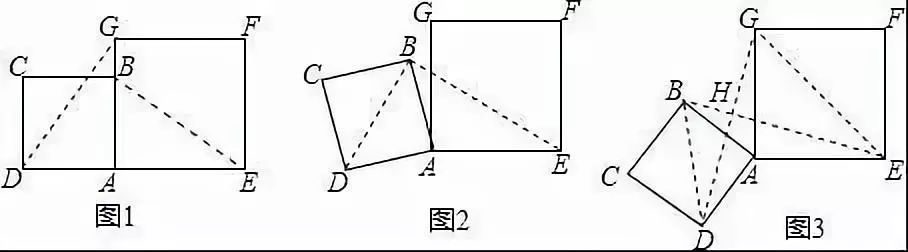
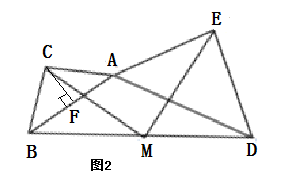
例2 现有两个具备一个公共顶点的等腰直角三角形△ADE和△ABC,其中ACB和AED=90,且AC=BC,AE=DE,CFAB于F,M为线段BD中点,连接CM,EM.(1)如图1,当A、B、D在同一条直线上时,若AC=1,AE=2,求FM的长度;(2)如图1,当A、B、D在同一条直线上时,求证:CM=EM;(3)如图2,当A、B、D在同一条直线上时,请探究CM,EM的数目关系和地方关系,请先给出结论,然后证明。